Ce puzzle triangulaire célèbre défie votre sagacité
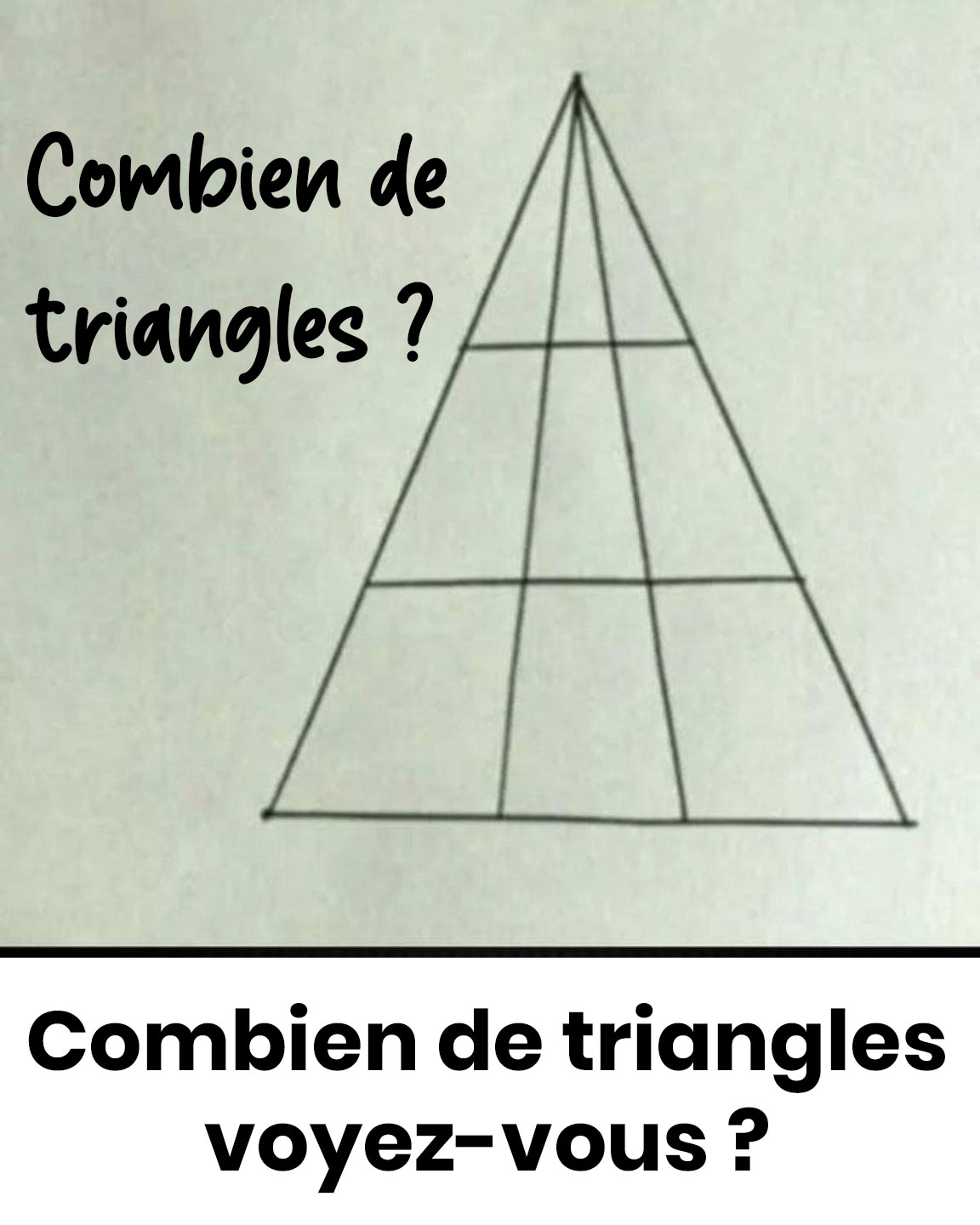
Sous ses apparences de forme géométrique élémentaire se cache une subtilité qui échappe au premier regard. Découvrez pourquoi tant de personnes échouent à résoudre cette illusion d'optique captivante qui semble simple en surface.
Le mystère des triangles cachés
Notre œil a cette fâcheuse habitude de ne retenir que les formes triangulaires les plus évidentes, en laissant de côté celles qui naissent de l’association de plusieurs éléments. Résultat : nous avons systématiquement tendance à en oublier. Dans cette configuration traditionnelle (4 étages formés par 3 lignes parallèles au bord inférieur), le total exact atteint 27.
Si vous êtes arrivé à 26, vous avez probablement manqué un grand triangle composite – souvent une figure orientée vers le haut couvrant 3 niveaux, ou une variante latérale partielle.
Méthode pas à pas : compter sans se tromper

Repérez les triangles « tournés vers le haut » selon leur hauteur :
- Hauteur 1 niveau : 10
- Hauteur 2 niveaux : 6
- Hauteur 3 niveaux : 3
- Hauteur 4 niveaux : 1
Total partiel « orientés vers le haut » : 10 + 6 + 3 + 1 = 20.
Ajoutez maintenant les triangles « dirigés vers le bas » créés par l’intersection des lignes : 7.
Solution définitive : 20 + 7 = 27.
Petite astuce mnémotechnique : retenez « 20 pour le haut, 7 pour le bas » et vous éviterez l’écueil classique.
La formule mathématique simplifiée

Vous préférez une approche rapide ? Pour une figure triangulaire principale divisée en n rangées via des traits parallèles à la base (ici n = 4), cette équation fonctionne :
T(n) = n × (n + 2) × (2n + 1) ÷ 8
Avec n = 4 :
T = 4 × 6 × 9 ÷ 8 = 27
Ce nombre correspond exactement à notre décompte visuel. La beauté de cette formule réside dans sa capacité à prendre en compte toutes les combinaisons possibles, y compris les formes multi-niveaux. Idéal pour vérifier son raisonnement… ou briller lors d’une conversation animée !
Erreurs fréquentes (et comment les contourner)
- Compter « par étages » sans voir les grandes figures transversales : l’oubli typique concerne généralement un triangle de 3 niveaux.
- Oublier les triangles inversés (« vers le bas ») : moins visibles à première vue, mais bien présents (7 au total).
- Imaginer des lignes verticales supplémentaires : certaines versions en comportent effectivement, ce qui modifie le résultat (mais jamais pour arriver à 26). Vérifiez toujours la structure exacte avant de conclure.
- Compter deux fois certaines formes : adoptez une progression méthodique par taille pour éviter les doublons.
Vous souhaitez aller plus loin ?
- Changez le nombre de niveaux : testez la formule avec n = 3 ou n = 5 et comparez avec un comptage visuel – excellent pour affuter votre regard.
- Lancez-vous un défi chronométré : accordez-vous 60 secondes pour trouver 27. Le secret ? Comptez d’abord les « supérieurs », puis ajoutez les « inférieurs ».
- Partagez l’astuce : expliquer une méthode, c’est la graver durablement dans votre mémoire (et assurer votre succès lors des prochains défis intellectuels).
Car derrière une apparence géométrique simple se cache souvent une leçon de logique appliquée… et cette délicieuse satisfaction de maîtriser parfaitement son sujet !









